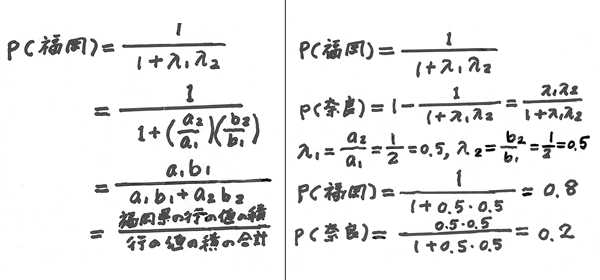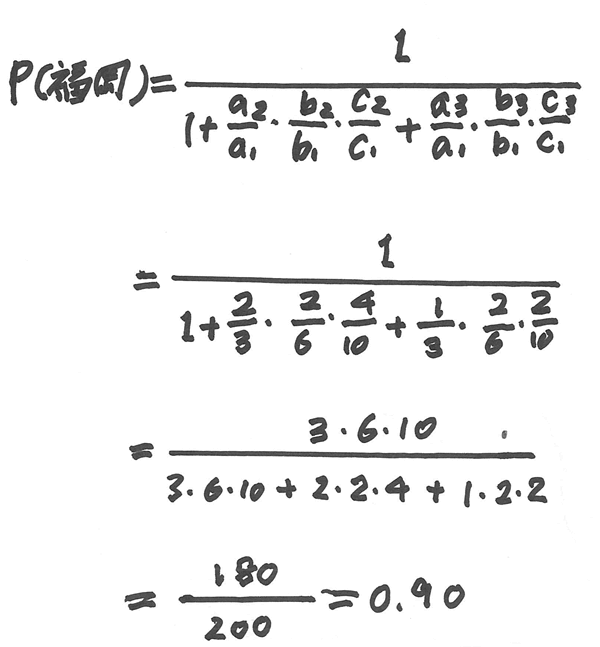| TOP>活動記録>講演会>第428回 | 一覧 | 次回 | 前回 | 戻る |
 |
 |
 |
 |
Rev2 2025.10.19 |
第428回 邪馬台国の会(2025.3.25 開催)
| ||||
1.邪馬台国問題解決への道 |
ある説が正しい、とはどういうことか。
数理歴史学の基礎論。 最近のデータサイエンスの進歩は目をみはるものがある。 これらのゲームでは、一手一手について、最終「勝率(勝つ確率)」を、コンピュータが示すことができる。さらに、コンピュータ同士を戦わせて、より勝率の高いソフトウェアを開発することができる。「勝率」にみちびかれ、文字どおり、機械的に打つ手が定められて行くのである。 京都大学大学院文学研究科准教授の大塚淳(おおつかじゅん)氏の手になる『統計を哲学する』(名古屋大学出版会、2020年刊)という本がある。 「現代において統計学は、与えられたデータから科学的な結論を導き出す装置として、特権的な役割を担っている。良かれ悪しかれ、『科学的に証明された』ということは、『適切な統計的処理によって結論にお墨付きが与えられた』ということとほとんど同義なこととして扱われている。しかしなぜ、統計学はこのような特権的な機能を果たしうる(あるいは少なくとも、果たすと期待されている)のだろうか。 ここで注意注目すべき事は、AI[Artificial Intelligence(人工知能)]将棋などにしても、ベイズ統計にしても、統計学的検定理論にしても、「確率」を求めることが、基礎をなしていることである。AI将棋などは「勝率」という形で「確率」を求める。ベイズ統計学では、「邪馬台国が福岡県にあった確率」「奈良県にあった確率」などの形で確率を求める。統計学的検定論では、種々の仮説のうち、一定の確率(ふつうは、1%、または、5%)以下の確率でしか成立しない仮説は捨てる(棄却)する約束をもうけることによって話を進める。そうしないと、「どんな小さな確率でも成立しないとは言えない」というような議論を強固に主張する人が出てきて、議論に決着がつかなくなるからである。つまり、仮設の取捨を客観的に行う装置として、「確率」を求める。鍵は「確率」にある。このことは、重要である。(哲学の問題ではなく、数学的、客観的基準を定める問題ではないか?)
■統計的方法の論理 いま、ある人が、「私は、十円玉を投げて、十回つづけで表をだしてみせる」といって、十円玉を投げ、ほんとうに、十回つづけて表をだしてみせたとする。 ☆仮説H1 この十円玉には、なにか、インチキなしかけがある。 そして、つぎに、この「仮説」を「検証」するために、その十円玉をしらべたり、その人の投げる手順をしらべたりする。 あるいは、つぎのような「仮説H2」をたてる人もいるかもしれない。 ☆仮説H2 これは、「偶然」によって、十回つづけて表がでたのだと考える。 そして、それ以上の探究は、放棄してしまう。このばあいに、なにを「偶然」と考えるかを、本人の「主観」にまかせると、「偶然によって、十回つづけて表がでるはずがないと私は考える」と主張する人もあらわれるであろうし、議論の決着が、つかなくなってしまう。 統計学、あるいは、確率論による判断の論理では、このようなばあい、一般に、まず、つぎのような形の「仮説」をたてるのである。この仮説(帰無仮説)をH0としよう。 ☆仮説H0 この十円玉の投げ方には、インチキはないと考える。 そして、つぎに、この仮説にもとづいて、論理を「演繹」するのである。すなわち、この「仮説」のもとでは、十円玉が十回つづけて表を出すことは、どれくらいの確率でおきるかを計算する。 「仮説H0」にもとづけば、この十円玉には、とくべつなインチキなしかけはないと考えるのであるから、表がでる可能性も、裏がでる可能性も、一応、ほぼ同じであると考えてよいであろう。すなわち、この十円玉の表がでる確率は、一応、二つに一つという意味で、1/2としてよいであろう。すると、十回つづけて表がでる確率は、 (1/2)↑10=1/1024 となる。 この1/1024という確率は、ふっうでは、まず、ちょっとおきないぐらいの小さな確率である。そのように小さな確率でしかおきないことが、偶然によっておきるのは、不自然である。そして、現代の統計学では、このようにしてえられた確率が、「5/100」または「1/100」よりも小さければ、もとの「仮説H0」をすてるという「約束」をもうけている。1/1024は、5/100よりも小さいし、また、1/100よりも小さい。したがって、もとの「仮説H0」は、すてさることになる。 すなわち、結論的には、 常識的な「仮説H1」のように、はじめに、「この十円玉の投げ方には、インチキなしかけがある」としてしまうと、それ以上論理を演繹することができなくなってしまう。そして、その仮説のもとでは、十円玉をしらべるとか、十円玉を投げる手順をしらべるとかする以外に、手がなくなってしまう。 「仮説H0」すなわち「この十円玉の投げ方には、インチギなしかけはない」のように、結論的には否定されることを予想してもうけられる仮説を、「帰無仮説[null hypothesis(ナル ハイポシシス)」という。 そして、この仮説が否定されたばあいには、私たちは、「この十円玉の投げ方には、インチキなしかけがある」と、「積極的に」主張できることになる。そして、私たちは、この結論が、どのていどの確からしさで成りたつかも、数字で知ることができる。すなわち、この結論が、絶対に正しいとは、いえないけれども、この結論が誤りであることは、百回に五回(5/100)、または、百回に一回(1/100)以下の割合でしか起きないという保証があるのである。このようにして、仮説の取捨の基準をさだめ、議論の客観化をはかるのである。確率は、カケ算できいてくるので、十円玉の問題のようなばあい、十回も試行すれば、十分、仮説の取拾の客観的判断ができる。だれが計算しても、同じ結果がえられる。つまり、「再現性」のある結果がえられる。 データサイエンスの骨格をなす統計学は、イギリスの統計学者、フィッシャー(Fisher,R.A.1890~1962)によって、1920年代に、いわゆる「推計学(推測統計学)」が提唱され、大きな変革がもたらされた。それまでの統計学は、観察・記述の学であったものが、確率論にもとづいて、推測の方法を与える学となった。実際の問題を解決する学となった。
■ベイズの統計学 計量言語学の手法とその成果 安本美典著 本書の著者はたいへん幅広い分野で活躍しておられ、そのご専門は分野名で特定し難いのですが、強いて言うと、応用数理学でありましょうか。近頃は、邪馬台国の問題など、日本の歴史に関係した分野での活躍が目立ちますが、日本語、とくにその起源の問題は、氏が以前から研究し、多数の著作を発表してこられた、おそらくメインの分野の一つではないかと思います。 さて、『言語の科学』と題する本書は、科学的手法での言語研究を目指した計量言語学を紹介したものです。この学問は、外国ではもうかなり確定したものなのですが、残念ながら、日本ではあまり知られていないようです。それで、それを紹介したい、ということです。副題は「日本語の起源をたずねる」ですが、「行動計量学シリーズ」の広告の中では、「比較言語学の新しい方法」となっています。実際、計量的な手法による、言語比較のたくさんの成果が具体例として示されています。その中には日本語も入っています。そして、その最後に、それらの成果を眺めて、日本語の起源についてどのように考えられるかを、比較的に簡単に、述べてあります。 つまり、計量言語学の中の言語比較の分野の紹介書です。たとえば、日本語と朝鮮語は親戚と言えるかどうか、というような問題がありますが、言語間の「近さ・遠さ」を議論する分野の紹介です。そのような言語比較では、数理的な裏づけをしない議論が多いのですが、比較のための計量化の方法をいろいろと、そして綿密に、解説しています。
■「統計的再現性」について このように、科学というのは民主主義に類似した仕組みで成り立っている。この成り立ちだけを広義に『科学』と呼んでも良いくらいだ。なにも、数学や物理などのいわゆる理系の対象には限らない。たとえば、人間科学、社会科学といった分野も現にある。 「まず。科学というのは『方法』である。そして、その方法とは、『他者によって再現できる』ことを条件として、組み上げていくシステムのことだ。他者に再現してもらうためには、数を用いた精確なコミュニケーションが重要となる。また、再現の一つの方法として実験がある。」
「各県ごとに、弥生時代後期の遺跡から出土する『鏡』『鉄の鏃』『勾玉』『絹』の数を調べて、その出土する割合をかけあわせれば、県ごとに、邪馬台国が存在した可能性の確率を求めることが可能になります。その意味では、邪馬台国問題は、ベイズ統計学向きの問題なのです」(「邪馬台国を統計学で突き止めた」『文藝春秋』2013年9月号) 私も、松原望教授との共同研究の成果をまとめ、『データサイエンスが解く邪馬台国--北部九州説はゆるがない--』(朝日新書、朝日新聞出版、2021年刊)などの形で本にした。
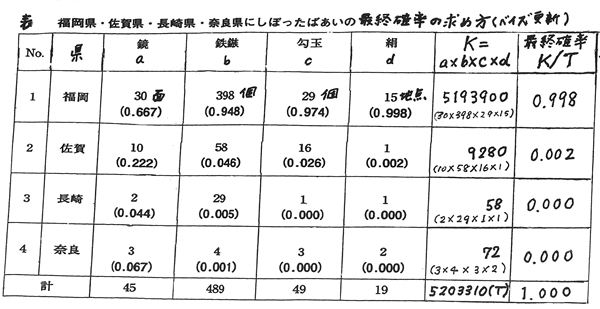
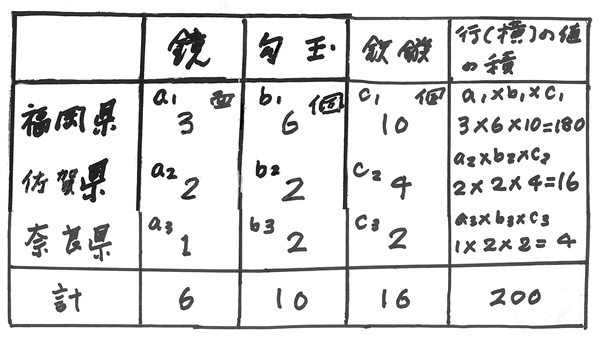
■ベイズの定理の証明 第418回2025年3月31日邪馬台国の会の講演のさいに配布した資料から、下図の表(福岡県・佐賀県・長崎県・奈良県にしぼったばあいの最終確率の求め方)がある
関連遺物が多いほど、それが邪馬台国の地である可能性(確率)が大きいとすれば、福岡県に邪馬台国が存在した可能性は10×100=1000倍となる。奈良県にあった可能性は1/10×1/100=1/1000となる。
☆ベイズの統計学により確率を求める(A)(B)(C)(D)の四とおりの方法 一般的に、数学の幾何で使うピタゴラスの定理は知っているが、「ピタゴラスの定理が正しいことを証明せよ」と言われと、ちょっと考えてしまうはず。そして、ピタゴラスの定理は証明の仕方が幾通りもある。 同じように、ベイズの定理は簡単に計算できる。そしてその証明方法は幾通りもある。その例を示してみたい。 ・与えられたデータ(出土数)をもとに確立を計算する。 (A)行(横)の値を順次掛けて行き、県ごとの値を求め、その値を、県ごとの値の合計値で割る方法。
(B)ベイズの公式による方法。 ベイズの定理は邪馬台国の会第416回講演を参照
すると、下の式になり、ベイズの公式により求められる。
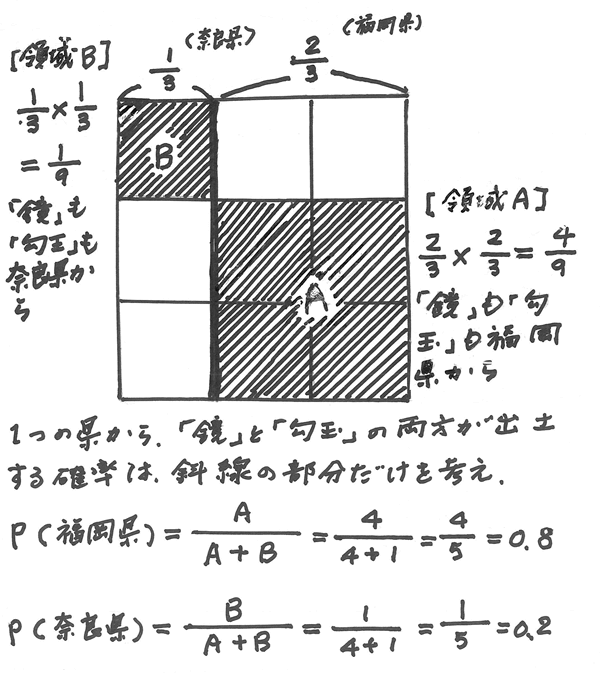
(D)図による方法
このように、(A)(B)(C)(D)の4つの方法を示した。 ・県の数と、遺物の種類数とを、ふやしたばあい
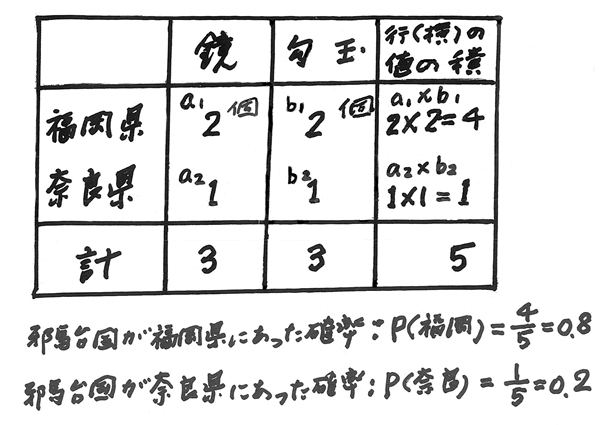
(A)行(横)の値を順次かけて行き、県ごとの値を求め、その値を県ごとの値の合計値で割る方法。
(B)ベイズの公式による方法。
他の県の値も同様にして求められる。
以上のように見てくると、(A)の、行(横)の数値を掛け合わせた数値は、「鏡」「勾玉」「鉄鏃」の3つがともに出てくる場合の数を数えるものであり、「鏡」と「勾玉」と「鉄鏃」がともに出土するという条件のもと(条件付き確率)で、「福岡県」なら「福岡県」が占める空間(面積)の大きさを示していることになる。
|
| TOP>活動記録>講演会>第428回 | 一覧 | 上へ | 次回 | 前回 | 戻る |